L'APL (initialement A Programming Language, officieusement Array-Processing Language[1]) est un langage de description de traitement de l'information devenu ensuite langage de programmation conçu entre 1957 et 1967 à Harvard par Kenneth Iverson pour décrire commodément des opérations globales sur des tableaux (booléens, numériques ou, dans une moindre mesure, de caractères). Iverson décrivait la grammaire de son langage comme similaire à celle d'un langage naturel (substantifs, verbes, adverbes, conjonctions, copules et ponctuation)[2]. Le langage n'utilise cependant pas de mots, mais beaucoup de signes, chacun correspondant à un concept précis[3]^,[4].

Cette page contient des caractères spéciaux ou non latins. Si certains caractères de cet article s’affichent mal (carrés vides, points d’interrogation, etc.), consultez la page d’aide Unicode.

Pour les articles homonymes, voir APL.

APL
Date de première version	1966
Paradigme	matriciel, Fonctionnel, Programmation structurée, tacite
Auteur	Kenneth E. Iverson
Développeur	Larry Breed, Dick Lathwell, Roger Moore et al.
Dernière version	ISO/IEC 13751:2001 (1er février 2001)
Typage	dynamique
Influencé par	Notation (mathématiques)
A influencé	Langage J, Matlab, A+
Implémentations	APL\360 APL\1130 APL*Plus Sharp APL APL2 Dyalog APL NARS2000 APLX GNU APL
Système d'exploitation	Multiplate-forme, Windows, GNU/Linux, Mac OS X
Licence	propriétaire, GPL
Extensions de fichiers	.apl
modifier

Révolutionnaire à son lancement (usage du terminal à boule ou à écran alors que la carte perforée ou le télétype ASR33 (en) restaient encore la référence, aucune déclaration nécessaire, typage et dimensionnement des variables inutile, gestion dynamique de mémoire, interactivité totale, concision par traitement direct des tableaux évitant l'écriture de boucles, persistance), il connut un succès croissant jusqu'au milieu des années 1980, époque où le tableur le concurrença pour les petits travaux, et des outils comme SAS, puis R pour le travail sur de plus grands volumes de données que ceux des tableurs de 1985.

En 2020, la disponibilité de processeurs très rapides adressant plusieurs gigaoctets de mémoire vive et l'existence d'interpréteurs Open Source peuvent le rendre à nouveau intéressant pour un public de passionnés[5]^,[6]. Rob Pike, créateur du langage Go, en parle en 2014 avec enthousiasme[7] et en 2020, il livre au public le code source du langage Ivy, une fondation d'APL en langage Go[8].

Dans sa version GNU APL, il est même utilisable comme langage de script.

• Le langage APL de départ fait l'objet de la norme ISO 8485 (1989).
• L'APL étendu (fondé sur APL2) est fixé par la norme ISO/CEI 13751 (2001).

Note : Vérifiez que votre navigateur accepte bien l’Unicode ; dans le cas contraire, vous verrez s’afficher des rectangles blancs ou des points d’interrogation à la place des caractères APL. Cette question est détaillée sur la Toile[9]. Aujourd'hui (2017) les navigateurs sur PC comme Mozilla Firefox ou Microsoft Edge ne posent aucun problème pour afficher les caractères APL en Unicode. Quelques problèmes d'affichage résiduels subsistent encore sur tablettes Android.

Historique

Les exemples sont donnés en double : une forme de copie d'écran dont le rendu sera correct quel que soit le navigateur que vous employez, et une en forme de texte que vous pouvez copier/coller par exemple dans NARS2000 (voir plus bas) pour l'exécuter, éventuellement avec quelques variantes. Le rendu de la page dépendra de votre police et de votre niveau de zoom par défaut. Vous pouvez les modifier, par exemple sur un PC par Ctrl+molette de la souris, en fonction de la résolution de votre écran.

Un historique en anglais d'APL est donné en PDF dans IBM Systems Journal, volume 30, n^o 4 (1991)[10]. Un décrivant ses progrès depuis 1978 existe également[11].

APL s’est montré particulièrement adapté dès ses débuts aux calculs statistiques, aux ventilations, aux consolidations, aux descriptions fonctionnelles d’architectures comme celle de l’IBM 360, aux graphiques interactifs (GRAPHPAK) et à quelques travaux en combinatoire et en théorie des graphes. Il a également été utilisé pour le prototypage d’applications et l’écriture de langages de manipulation simples dans le cadre d’un infocentre en masquant les symboles appropriés sous des dénominations commodes et parlantes, par exemple en permettant d’écrire simplement :

MOYENNE X pour (+/X)÷⍴X.
"(Somme des éléments de X), divisée par le nombre d'éléments de X)"

NORMALISER X pour X÷+/X
"Diviser chaque élément de X par la somme de tous les éléments de X" etc.

Si l'on envisage des tableaux gigantesques, la notion de MapReduce n'est pas loin[12], et de fait plusieurs implémentations d'APL utilisent, sans que l'utilisateur ait à en coder l'utilisation lui-même, le parallélisme du matériel (voir plus bas).

Il permet de manipuler aisément des tableaux de N dimensions (N variant de 7 à 255 selon l’implémentation considérée, avec des tailles de 0 à 65000 et plus sur chaque dimension) de façon globale. Les opérations puissantes, calculs de feuilletage (lamination) ainsi que les opérateurs de réduction /, expansion \, produit intérieur . et produit extérieur ∘. et les opérations de compression / évitent souvent toute nécessité d’indices de boucle explicite - ainsi d’ailleurs que l’usage de boucles lui-même.

Iverson insistait sur le fait qu'APL était un langage de pensée tout autant qu'un langage de programmation. C'est en effet une notation mathématique rigoureuse et concise[13].

Les symboles APL représentant des opérations utilisables en programmation comme en calcul immédiat à la console, par exemple le « domino » ⌹ qui inverse directement une matrice carrée, ou résout un système d’équations linéaires surdimensionné au sens des moindres carrés si la matrice est rectangulaire :

      a←2 2⍴⍳4
      ⌹a
¯2    1  
 1.5 ¯0.5

On estimait dans les années 1970-80 qu’une équipe de 5 développeurs APL avait la puissance de développement d’une équipe de 25 programmeurs FORTRAN[14]. L’application APL se montrait plus gourmande en ressources matérielles, mais le prix de celles-ci était en constante diminution. En 2013, son adaptation à la programmation agile lui donne un regain d'intérêt pour toutes les applications à mettre en place ou faire évoluer rapidement, aussi bien que pour les applications à courte durée de vie. Il a été utilisé entre autres[15] par la NASA, British Airways, la Banque de France (études économiques éclair), la Direction générale des Finances publiques française (impact fiscal de lois nouvelles), etc.

Après avoir connu le creux de la vague en 2009, l'intérêt pour ce langage remonte significativement depuis[16].

Depuis 2013 également, il est proposé pour la réalisation de servlets[17].

Son interface initiale (bicolore en mode machine à écrire) a inspiré celle de logiciels comme Maple.

Présentation

APL innovait à son lancement par plusieurs aspects conviviaux :

• pas de déclaration de types ni de réservations de taille, une variable contenant tout simplement ce qu’on a mis dedans (scalaire ou tableau ; booléens, entiers, caractères ou nombres flottants) ;
• possibilité d’interrompre un programme, d’interroger et de modifier des variables, et de reprendre l’exécution ; ou bien de tout stocker en l’état et de reprendre le lendemain en retrouvant les objets de la zone de travail — fonctions, variables et états d’exécution — exactement comme on les avait laissés (bref, de la persistance avant la lettre… dès 1969 !) ;
• gestion dynamique de mémoire automatique ;
• pas de syntaxe compliquée pour afficher des résultats : quand un résultat est calculé sans être envoyé ensuite dans une variable, alors il est affiché simplement au terminal dans le format estimé le plus lisible.

Exemples

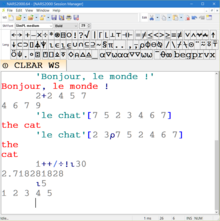
Ainsi pour écrire « Hello, World! » en APL, les choses se passent ainsi :

'Bonjour, le monde !' ⍝ tapé par l’utilisateur

Bonjour, le monde ! ⍝ réponse du terminal

2+2 3 5 7 ⍝ donne

4 5 7 9

Il faut y ajouter la possibilité spectaculaire d’indexer un tableau par un autre tableau. Ainsi :

'LE CHAT'[7 5 2 3 4 6 7] ⍝ donne

THE CAT

Voire :

'LE CHAT'[2 3 ⍴ 7 5 2 4 6 7] ⍝ donne

THE
CAT

Pas de traduction automatique ici ni dans un cas ni dans l'autre : l'indice a simplement été remplacé par ce qui était indicé (ainsi T est le septième caractère), ce qui est le propre de l'opération d'indexation. Ce qui est indicé prend également la forme de l'indice (ainsi, une matrice 2x3 dans le second cas)[18].

Grâce à sa priorité de droite à gauche, le langage se lit simplement, comme une langue naturelle : « 1 plus somme des inverses des factorielles des entiers de 1 à 30 » s'écrira :

1++/÷!⍳30 ⍝ qui donne

2.718281828

Le même résultat (c'est-à-dire la valeur de e) peut s'obtenir en frappant directement *1, ce qui signifie exponentielle 1.

L'APL des origines ne connaissait que scalaires et tableaux (numériques ou de caractères). Il gère maintenant des tableaux de tableaux et permet également à l'utilisateur de définir lui-même ses propres « opérateurs »[19].

Il travaille également en nombres complexes automatiquement si les besoins du calcul le demandent. La valeur ${\displaystyle i}$ s'écrit 0J1​ et en conséquence 0J1*2​ donne ¯1J0​. NARS2000 reconnaît pour sa part non seulement les nombres complexes, mais également les quaternions[20]^,[21] : si l'on écrit 0+1J, le système l'imprime - et l'interprète - comme 0i0j1k0 et 0i0j1k0*2 vaut bien entendu ¯1i0j0k0. Les octonions sont également supportés (1i2j3k4l5ij6jk7kl8).

Opérations sur tableaux

Le caractère ⎕ se lit "quad".

⎕←A←2 2⍴⍳4 ⍝ imprime une matrice A de taille 2x2 constituée des nombres de 1 à 4

1 2

3 4

A=2 ⍝ donne une matrice booléenne indiquant les éléments de A égaux à 2

0 1

0 0

A, A ⍝ concatène, horizontalement, la matrice A avec elle-même, formant une matrice de 2x4

1 2 1 2

3 4 3 4

A, 5 ⍝ concatène le scalaire 5 à la matrice A

1 2 5

3 4 5

A, +/A ⍝ concatène verticalement (⍪) à A un vecteur 'somme de A par colonnes' (+/A)

1 2 3

3 4 7

A⍪+⌿A ⍝ donne

1 2

3 4

4 6

même chose suivant l'autre axe : colonnes

A, [.5]0 ⍝ donne

1 2

3 4


0 0

0 0

concaténation en créant une nouvelle dimension : la matrice devient cube

A, [1.5]0

1 2

0 0


3 4

0 0

Cette opération a créé une nouvelle dimension sur un autre axe.

Le produit externe alias cartésien, crée des tableaux à partir de vecteurs, à la manière d'une table de multiplication :

      1 2∘.+10 20 30
11 21 31
12 22 32
      ⎕←a←,1 2∘.+10 20 30
11 21 31 12 22 32
      a[⍋a]
11 12 21 22 31 32

La primitive ⍋, que l'on nomme grade-up, fournit la permutation qui classe en ordre croissant les éléments d'un vecteur (et non ce vecteur classé lui-même). En d'autres termes, a[⍋a] renvoie toujours un vecteur trié, et ⍋a toujours un vecteur de permutation formé des éléments de ⍳⍴a permutés, ce qui constitue un moyen concis et économique de créer et combiner des permutations[23]. De telles permutations s'obtiennent facilement par tirage exhaustif : 52?52 pour un tirage de 52 cartes parmi 52.

Opérations sur les ensembles

Les symboles ensemblistes (∊, ∪, ∩, ⊆, ⊇, ⍦...) existent en APL, et font l'objet d'extensions particulières permettant de travailler en ensembles simples (dont chaque élément d'apparaît qu'une fois) ou bien multisets dont chaque élément peut apparaître plusieurs fois, utiles pour les combinaisons de Bose-Einstein[24]

Selon que les éléments de ces ensembles possèdent une identité propre ou au contraire non (c'est-à-dire sont indiscernables), il existe douze façons bien distinctes (en) de traiter les ensembles.

Opérateurs

De même qu'une fonction agit sur une ou plusieurs variables, un opérateur agit sur une ou plusieurs fonctions (ou opérations). Pour prendre une comparaison mathématique, « sigma » et « pi » correspondent à l'opérateur APL de réduction (« / ») appliqué aux opérations « + » et « × ». Sigma (somme de termes) s'écrit +/, « pi » (multiplication entre termes) ×/, « union » (ou logique entre termes) ∨/, « conjonction » ("et" logique entre termes) ∧/, etc. On parle, dans d'autres langages, de clôture (closure).

Dans la première version d’APL, les opérateurs sont définis de façon fixe (réduction (/), scan (\), produit externe (°.), composition (.)...). En APL2, l’utilisateur peut fabriquer les siens à volonté et leur donner des noms. Un opérateur peut agir indifféremment sur des opérations de base du langage ou sur des fonctions définies par l’utilisateur dans son workspace.

APL2 introduit également l'opérateur tréma (¨, nommé each), généralisant au niveau de chaque sous-tableau une opération dans les tableaux de tableaux.

      ⍳4
1 2 3 4

      ⍳¨⍳4
 1  1 2  1 2 3  1 2 3 4

      ⍝ La fonction système ⎕fmt ("quad fmt") affiche cela plus clairement
      ⎕fmt ⍳¨⍳4
┌4──────────────────────────┐
│┌1┐ ┌2──┐ ┌3────┐ ┌4──────┐│
││1│ │1 2│ │1 2 3│ │1 2 3 4││
│└~┘ └~──┘ └~────┘ └~──────┘2
└∊──────────────────────────┘
     
      ⊃⍳¨⍳5
1 0 0 0 0
1 2 0 0 0
1 2 3 0 0
1 2 3 4 0
1 2 3 4 5

      ⎕fmt ⊃⍳¨⍳5
┌5────────┐
51 0 0 0 0│
│1 2 0 0 0│
│1 2 3 0 0│
│1 2 3 4 0│
│1 2 3 4 5│
└~────────┘

      6 2⍕⌹⊃⍳¨⍳5
  1.00 ¯0.00  0.00 ¯0.00  0.00
 ¯0.50  0.50 ¯0.00  0.00 ¯0.00
 ¯0.00 ¯0.33  0.33  0.00  0.00
  0.00  0.00 ¯0.25  0.25 ¯0.00
 ¯0.00 ¯0.00  0.00 ¯0.20  0.20

Voir note [25].

Tableaux de tableaux, et fonction ⍎

Une opération nommée enclose (⊂) permet d’encapsuler un tableau qui est alors vu comme un scalaire. Il est dès lors facile de représenter des structures complexes sous forme de tableaux ayant pour éléments d’autres tableaux. L’existence d’une fonction execute (⍎)[26] permet même d’inclure dans ces tableaux de tableaux des désignateurs de fonction que l’on peut exécuter à la demande, comme en langage C. Elle permet aussi à un programme d’engendrer lui-même un code qu’il exécutera ensuite, comme en Lisp ou en Haskell : les fonctions sont alors juste des types de variables particuliers. Voir programmation fonctionnelle.

Le nombre d'indices d’un tableau est par convention nommé rang (rank) en APL (à ne pas confondre avec le rang d'une matrice en algèbre linéaire) et est toujours retourné par ⍴⍴. Le nombre de niveaux d’un tableau de tableaux est nommé profondeur (depth) et retourné par ≡.

Espace de travail

L’utilisateur travaille dans un espace de travail (workspace) où il stocke ses fonctions et ses variables. Il peut à tout moment sauvegarder l’ensemble (y compris en état d’exécution suspendue) et reprendre plus tard son travail exactement dans les conditions où il l’avait laissé, y compris dans l'état où il aurait interrompu un programme en cours[27]. Des commandes comme )COPY et )PCOPY, et la notion de groupe permettent des transferts aisés de fonctions et de variables d’un workspace à un autre (un groupe est un nom donné à un ensemble de fonctions et de variables qui travaillent ensemble, permettant de les importer toutes en même temps sans détailler leurs noms ni importer tout l'espace de travail).

Les APL commerciaux sont fournis avec plusieurs bibliothèques d'espaces de travail d'exemples, exécutables et modifiables. En APL2 d'IBM, ces bibliothèques portent des numéros )LIB 1, )LIB 2, etc. (voir figure de gauche).

Horodatage automatique

Chaque objet APL2 (variable, fonction ou opérateur) est automatiquement horodaté dans l'espace de travail (workspace), ce qui facilite sa gestion sur le long terme. Le type et la date des objets sont retournées par la fonction système ⎕AT (=ATtributes). Couplé aux opérations de tri ⍋ (grade-up) et ⍒ (grade-down), cet horodatage des objets facilite beaucoup le processus de développement.

⎕NL (=Name List) ramène la liste des éléments de la zone de travail, ⎕NL 3 ramène la liste de ses seules fonctions. Comme on le voit, la concaténation horizontale de tableaux de nature différente juste par une virgule rend aisés les affichages.

En NARS2000, la fonction système ⎕vr liste de plus une fonction avec ses numéros de ligne, la dernière ligne contenant son horodatage. Le résultat est un simple vecteur de caractères contenant quelques caractères de retour ligne, la colorisation standard des caractères étant effectuée par le système

Éléments historiques

• APL travaillant sur des vecteurs, il devait distinguer l’opération « - » (moins), désignant l'opération de soustraction d'un opérande numérique (dimensionné ou non) ou son changement de signe du simple signe négatif qui ne porte que sur le scalaire qui le suit immédiatement, d'autre part. Celui-ci est noté par une barre supérieure « ¯ ».

Ainsi, 7 5 6 - 4 3 2 produit 3 2 4, mais 7 5 6 ¯4 3 2 produit… 7 5 6 ¯4 3 2

• Lorsqu’APL tourne sur un système, par exemple le RS/6000, on s’écarte de la tradition en le nommant non pas APL/6000, mais bien APL\6000. Pourquoi ? Parce que « / » est un opérateur de réduction et que « \ » est l’opérateur d'expansion. Logique.

• APL était au départ utilisé uniquement en interne par IBM, sans plan de commercialisation. Selon Yves Le Borgne, la NASA fit toutefois pression pour que ce langage fût mis à sa disposition, menaçant de changer de constructeur si elle n’obtenait pas satisfaction. Le langage fut mis timidement au catalogue en 1969 à titre de produit complémentaire, puis en quelques années prit le statut de langage stratégique, qu’il garda jusqu’en 1990 (à partir de cette date, ne pouvait plus être considéré comme stratégique un langage ne tournant pas sur toutes les plateformes, et porter APL sur l’AS/400 ne présentait pas d’intérêt pour le créneau spécifique de cette machine, essentiellement les besoins de gestion d'entreprises de taille moyenne).

Idiomes APL

Les tournures idiomatiques APL les plus utiles furent collationnées dans les universités au moins depuis 1977[28] et leur liste reste mise à jour sur un wiki[29] en Unicode.

Quelques-unes de ces tournures concernent le premier APL, qui ne possédait pas les tableaux de tableaux; elles restent valides aujourd'hui, bien qu'APL2 permette d'en simplifier plusieurs. IBM met à disposition une version adaptée à APL2[30], dont les exemples peuvent être copiés/collés dans un interpréteur, ainsi que l'espace de travail IDIOMS dans son TRYAPL2 gratuit destiné au DOS ou à une DOSBox quelconque. Dyalog APL met à disposition sa propre liste[31]. Les consulter est utile pour se familiariser avec le mode de pensée propre à APL et découvrir concrètement l'usage de ses primitives et opérateurs.

Stanley Jordan a présenté à l'ACM une communication sur l'usage de phrases APL pour assister la composition musicale[32]

Enfin, le site rosettacode donne plusieurs exemples de petits problèmes avec leur résolution en APL ainsi que (de façon en général moins concise) dans d'autres langages : https://rosettacode.org/wiki/Category:APL

Implémentations

Gratuites

Quatre grandes implémentations en Open Source d'APL sont téléchargeables gratuitement :

• A+, dialecte d'APL disponible dans les dépôts standards de plusieurs distributions Linux, dont Ubuntu, sous le nom de aplus-fsf. Ce langage A+[33] ne doit pas être confondu avec la certification A+ de connaissances de base en usage de l'informatique. Intensivement utilisé chez Morgan Stanley[34]^,[35], il conserve des primitives APL comme le ⍳, mais remplace par exemple le ⍴ par #. Il possède aussi un mode de représentation ASCII où on écrit juste iota, rho, take, each, etc.
  • Page du langage A+

• GNU APL[36] directement utilisable sous Linux, ainsi que sous Windows au moyen de Cygwin. Le soin de charger une des polices de caractères APL dans la fenêtre correspondante est laissé cette fois-ci à l'utilisateur et celui-ci doit modifier son clavier soit avec setxkbmap soit avec xmodmap.
  • Page de GNU APL

Article détaillé : GNU APL.

• MVT for APL est un portage de l'APL\360 sur beaucoup d'autres plateformes y compris le Raspberry Pi[37], avec une trentaine d'espaces de travail (workspaces) dont une, PLOT, pour tracer des semigraphiques, le tout pour un usage strictement privé. Il utilise l'émulateur Hercules[38], livré avec l'ensemble.

• NARS2000[39], muni d'un installeur pour Windows, et disponible en versions 32 et 64 bits[40]. La version 0.4.5.68 a montré fonctionner également depuis Wine sous Linux[41] (voir illustration ci-contre)[42]. Historiquement, NARS est issu de travaux de la société STSC, Scientific Time-Sharing Corporation[43]. La version 0.5.8.8 disponible en décembre 2018 passe automatiquement si besoin les calculs sur entiers en entiers de précision illimitée par défaut, en lieu et place d'une représentation flottante (par exemple !508, factorielle 508; dont le résultat comporte 1156 chiffres). Les quotients de tels entiers géants sont conservés en interne sous forme de rationnels avec un numérateur et un dénominateur de précisions illimitées également. La version 0.5.19.0 de juillet 2019 autorise les espaces soulignés dans l'écriture des nombres (exemple 1_000_000) et introduit une nouvelle commande )BOX. )BOX OFF est le fonctionnement normal. )BOX ON réalise un ⎕fmt automatique pour chaque sortie.

La demande de calculs en précision illimitée[44] se fait en faisant suivre les constantes d'un suffixe x qui est propagé ensuite automatiquement dans tous les calculs où elles interviennent. Les variables ⎕pp (précision d'affichage) et ⎕fpc (précision des flottants) permettent de limiter la taille des affichages et la précision des flottants étendus à ce qui est jugé strictement nécessaire.

En 2020, la version alpha de NARS2000 permet le type de variable "intervalle"signalé par le suffixe ±, qui se propage à tous les calculs et fournit de ce fait la précision du résultat

Orienté recherche, NARS2000 se munit dans sa branche alpha (2020) de l'arithmétique d'intervalles en nombres entiers et son extension aux calculs matriciels avec des hypercomplexes en flottants de précision numérique arbitraire[45]ce qui permet de donner des résultats ± quelque chose dès lors que ce suffixe accompagne l'une des constantes du calcul. Chaque résultat est alors accompagné de sa fourchette de signification tenant compte des lacunes de la représentation flottante, et propagée dans tout calcul :

      (√2±)*2
2v±2.4E¯38v 
       ⎕fpc←200
       (√2±)*2
2v±5E¯60v 
      ⌹2 2⍴⍳4±
 ¯2v±6.6E¯60v    1v±3.7E¯60v
1.5v±4E¯60v   ¯0.5v±1.7E¯60v
      a⌹a←2 2⍴⍳4±
              1v±3.3E¯60v 0v±5E¯60v  
9.334522963E¯61v±1.4E¯60v 1v±3.7E¯60v

• Manuel d'initiation à NARS2000 (PDF, gratuit)

• OpenAPL, sur SourceForge[46] et mis à jour le 10 avril 2013.

Commerciales avec cas de gratuité

• Dyalog laisse son APL - et les espaces de travail qu'il y a associés - en libre téléchargement sous réserve d'un engagement sur l'honneur de ne pas l'utiliser à des fins commerciales et de ne pas le transmettre directement, afin sans doute de permettre une traçabilité fiable de ces téléchargements[47] Cette société se montre par ailleurs très coopérative avec les enthousiastes d'APL, engageant parfois de brefs dialogues par courriel avec certains d'entre eux. Google lui a réservé une place dans une de ses conférences annuelles[48].

• IBM, première société à avoir produit un APL, propose une version téléchargeable d'essai gratuite de son APL2 limitée à 5 heures de temps CPU, ce qui avec les processeurs de 2016 permet de six mois à un an d'essais personnels pour explorer le langage et les workspaces qui l'accompagnent. Cette version inclut un grand nombre d'espaces de travail qui rendent opérationnel rapidement, en particulier sur la création de graphiques vectoriels 2D et 3D (particulièrement aisés à représenter sous forme de matrices APL) avec Graphpak. Attention : sa répartition de clavier, aussi bien en AZERTY qu'en QWERTY, lui est propre et diffère légèrement des autres implémentations.

• MicroAPL fournissait une version gratuite de son produit APLX, limitée à 30 jours pour évaluation. La version Linux est cependant utilisable indéfiniment pour usages non-commerciaux[49]. La version Windows comportait un installeur[50]. En juillet 2016, MicroAPL arrête ses activités et confie à Dyalog le soin de les proposer avec un statut semblable à l'abandonware[51].

Diverses

Des interpréteurs APL ont existé pour l’IBM 7090, les IBM 360 à zSeries (sous TSO, VM/CMS et même CICS!), l’IBM 1130, le Xerox XDS Sigma 7 alias CII 10070, et le CII Iris 80, le Bull DPS-7, le Burroughs B5500, le Bull SEMS T1600 (ex-Télémécanique Électrique T1600), la série des Mitra, etc.

La Sligos avait écrit en 1976 un APL pour Iris 80 (CII) afin d'offrir ce langage en service de télétraitement. Le projet fut abandonné quelques mois après sa réalisation pour des raisons de performances insuffisantes lors de la montée en charge. Les espaces de travail destinés à la migration du 370 vers l'Iris 80 furent légèrement modifiés pour permettre la migration inverse.

APL était aussi fourni directement en ROM dans des ordinateurs personnels du début des années 1970 (avant Apple, donc) comme le MCM-70, qui possédait un affichage d'une ligne[52], ou l’IBM 5110 modèles A et C.

Des versions station de travail et ordinateur personnel en ont aussi été commercialisées ou réalisées gratuitement pour AIX, Solaris, Linux, Windows, Mac OS, OS/2. Il en existe même pour le DOS (version gratuite nommée TRYAPL2, en version anglaise comme française; la francisation a été réalisée par l'AFAPL[53])... ainsi que pour Android[54] !

La société Microsoft avait entrepris deux implémentations du langage sur 8080 et 6800, d'après une lettre de Bill Gates aux utilisateurs de l'Altair BASIC[55]. Le succès de DOS, de Windows et surtout des tableurs Multiplan et Excel fit abandonner ce projet, qui aurait eu un public potentiel bien plus restreint : le très grand public réclamait alors des applications clés en main (à l'exemple de VisiCalc sur Apple II) et non des langages pour les programmer eux-mêmes.

Environnements informatiques

Le mécanisme d’échange dit des processeurs auxiliaires permet à des workspaces APL de communiquer avec le monde extérieur : fichiers, SQL/DB2, TCP/IP, X-window, OpenGL, ainsi qu'autres workspaces APL et consoles du réseau actives au même moment si celles-ci en donnent l’autorisation. On peut ainsi commencer à mettre au point un calcul sur un PC, puis une fois qu’il est au point l’exécuter à distance sur un ordinateur central équipés de dizaines de processeurs parallèles depuis la même session sur PC.

Les processeurs auxiliaires permettent même à des sessions de station de travail de communiquer efficacement avec des sessions du même langage sur mainframe, ou encore entre elles. Des calculs matriciels de très grande taille peuvent ainsi être distribués en réseau.

Les processeurs auxiliaires se codent le plus souvent en langage C.

Quelques-uns livrés avec IBM APL2[56] sont AP124 (adressage direct de l'écran, genre curses), AP127 et AP227 (resp. accès aux bases de données DB2 et ODBC), AP144 et AP145 (resp. adressages X-Window et Windows), AP200 (coordinations de sessions APL distinctes), AP207 (processeur de graphiques interactifs, utilisé par GRAPHPAK).

Glyphes

Tous les caractères APL ne sont pas encore associés à une signification aujourd'hui (2020). GNU APL, Dyalog APL et NARS2000 en utilisent trois : ⍺ et ⍵, qui désignent le premier et le dernier argument d'une fonction, et λ qui en désigne le résultat. Exemple :

      )FNS
SUM

      ∇SUM[⎕]∇
[0] λ←⍺ SUM ⍵
[1] λ← ⍺ + ⍵ 

La définition de cette fonction se ferait par SUM ← { ⍺ + ⍵ }. Celle de moyenne se ferait de même par moyenne←{(+/⍵)÷⍴⍵}. Il s'agit bien de programmation fonctionnelle.

⍝ Surface d'un polygone en Dyalog APL

surface←{÷∘2⊢-/{+⌿×/⍵}¨(0 1)(1 0)⊖¨⊂⍵} ⍝ définit la fonction "surface"
surface↑⌽(0 3)(3 0)(0 0)               ⍝ applique cette fonction à un triangle donné
4.5

⍺ et ⍵ représentent ci-dessus les opérandes d’une fonction. De même et par convention ⍺⍺ et ⍵⍵ représentent les fonctions sur lesquelles s’applique un opérateur.

Quelques implémentations comme NARS2000 proposent des utilisations mathématiquement puissantes d'autres symboles[57].

Polices APL existantes

En mai 2010, les principales polices APL téléchargeables depuis l'Internet sont les suivantes[58] :

• APL385 Unicode (Dyalog APL)[59]
• APX Upright (MicroAPL APLX)
• Courier APL2 Unicode (IBM APL2)
• SImPL (NARS2000)

Les caractères Unicode APL2 sont définis dans l'un des plans de la police Arial[60], et permettent donc de copier/coller directement de l'APL depuis une session de calcul (voire une page web) dans un traitement de texte ou l'inverse, ce qui était impossible commodément avant l'Unicode.

L'Unicode APL, encodé en UTF-8, permet de :

• copier/coller des expressions et programmes APL depuis des pages web.
• les imprimer sous toutes les imprimantes actuelles
• se connecter par telnet ou ssh à des serveurs offrant un service APL
• rediriger (piping) des flots UTF-8 vers l'interpréteur APL, ce qui permet d'utiliser APL pour des scripts
• échanger des programmes avec des interpréteurs ou des utilisateurs APL utilisant d'autres APL.
• copier du code APL dans des documents.

Les navigateurs Web honorent depuis 2010 l'affichage des caractères APL. Beaucoup de tablettes en sont capables en 2015.

Clavier

La disposition du clavier APL d'origine pour les États-Unis avait été choisie pour des considérations mnémotechniques, par exemple ? associé au Q (Question mark) ⍴ (rho) au R, etc. Une question a été de savoir si le clavier APL français devait associer un caractère à la touche elle-même (? serait alors associe au A et non plus au Q) ou à sa signification (ce qui aurait eu pour effet de combiner les spécificités francophones aux spécificités d'APL.

• APL/APL2, d'IBM, a retenu la première solution.
• Dyalog APL propose ce clavier français. Les caractères APL s'obtiennent par composition avec la touche Ctrl. Quand on désire restaurer les comportements standards de Ctrl-X, Ctrl-Z, etc., cliquer sur le bouton FRA en bas à droite de la barre de tâches de Windows permet de commuter entre clavier français et clavier APL.
• GNU APL laisse le spécialiste X-window décider, s'il en a la compétence, des questions d'interface. Quelques configurations de clavier sont cependant fournies avec lui. Le basculement du clavier entre APL et français par la combinaison de touches Alt-CapsLock est expliqué dans l'article GNU APL.
• NARS2000 permet de configurer de façon graphique et interactive son clavier à la demande si on le désire, à partir d'un des modèles de dispositions fournis. Sa configuration de base du clavier français utilise les caractères existants et permet d'obtenir les autres par la touche Alt (Alt-i pour ⍳ (iota), Alt-r pour ⍴ (rho), etc. Seuls les crochets exigent l'usage du caractère de composition Ctrl).

La question est moins futile qu'elle ne le semblerait : l'usage d'APL demande beaucoup de concentration. Si lors des frappes de caractères cette concentration est interrompue par une interrogation sur la touche à frapper sur le clavier et/ou le modificateur à enfoncer (Shift, Alt ou Ctrl), l'usage de ce langage deviendra inefficace quelles que soient ses qualités au départ.

On peut aussi se créer une disposition de clavier sur mesures, que ce soit en Windows[61] ou en X-Window (setxkbmap -layout us,apl -variant ,dyalog -option grp:lswitch, au détriment cependant de l'interopérabilité si on vient à utiliser d'autres machines que la sienne.

Ce document de 5 pages détaille une implémentation possible de clavier APL sous Linux :

• (en) [PDF] Supporting APL keyboards on Linux

Autour du langage

Situation présente

L’apparition du tableur, plus intuitif et plus facile à manier, a fait disparaître une partie de l’intérêt du langage. Cela n’enlève rien pour autant à sa puissance d’expression et à sa concision, et plusieurs interpréteurs APL sont téléchargeables gratuitement sur Internet, pour le PC (Linux ou Windows) comme pour le Macintosh. Les caractères APL/APL2 sont présents dans l’Unicode[62].

APL traitant globalement les tableaux, ses implémentations tirent aisément parti des possibilités de calcul parallèle ou de pipeline des processeurs modernes. Elles utilisent extensivement les possibilités vectorielles du S/390 (zSeries), de l’architecture PowerPC (pipeline optimisé d'instructions similaires) et des instructions multimédia (SSE) de l’architecture Intel/AMD. Dans la mesure ou APL traite globalement les tableaux sans imposer le détail du traitement, plusieurs de ses primitives et opérateurs peuvent être implémentés en calcul parallèle CUDA, voire en calcul quantique[63], local ou distant si des circuits de calcul de ce type deviennent disponibles.

L'opérateur ∘ permet d'exprimer le produit cartésien entre deux vecteurs de données, donc toutes les combinaisons de leurs opérandes (opération en N^2) et ensuite l'opérateur / d'en comprimer le résultat selon une autre opération. L'ensemble exprime le calcul combinatoire demandé à ce calculateur, de même qu'une requête SQL exprime ce qui est demande à une base de données, sans avoir à rentrer dans le détail du calcul.

La version 17.0 de l'APL de Dyalog (juillet 2018) utilise automatiquement les instructions vectorielles des architectures x64, POWER et ARM[64].

Deux successeurs d'APL sont le langage A+^{[réf. nécessaire]}, et le langage J, ce dernier ayant été promu par K. E. Iverson lui-même, et ne nécessitant pas l’usage de caractères spéciaux. APL possède toutefois une lisibilité supérieure, à condition de disposer de la police de caractères appropriée. La mise à disposition du langage lui-même n’aurait pas été possible dès 1969 sans les terminaux IBM à boule également nommés Selectric (par exemple le 2741). Sur les terminaux purement alphanumériques 2260, il fallait utiliser des mots-clés peu lisibles. Les terminaux 3270, dès le 3277, ont permis par la suite les jeux de caractères APL ainsi que les minuscules latines.

Pour information, des calculs sur un Celeron 300 MHz de 2004 s’effectuent à peu près en un dixième du temps de calcul qu’ils prenaient en 1970 sur un IBM 360/91. Le cœur de l’interpréteur tient entièrement dans le cache d'instructions d’un microprocesseur contemporain (2020)[65], donnant à APL des performances en exécution comparables à celles de langages compilés, comme dans cet exemple :

      ⎕cr 'test'
test;s       
⎕ts          
s←+/÷⍳1000000
⎕ts          
      test
2016 5 7 14 20 52 301 
2016 5 7 14 20 52 350

On voit ici que le calcul du nombre harmonique H_1000000 prend 49ms (350 - 301) dans le time stamp[66]. Ce calcul a été réalisé sur un Core i7 4500U, passmark de 3800 environ[67]. Il prend 36ms sur un Core i7 4790 au passmark de 10000 (à comparer, sur cette seconde machine, avec 13ms pour le même calcul en langage C et, curieusement, 13ms aussi en Dyalog APL 64 bits version 15).

Graphpak est un des espaces de travail fournis avec l'APL d'IBM et combinable avec toute autre application de l’utilisateur pour lui donner des possibilités d’entrée-sortie graphiques 2D comme 3D. La structure des appels du langage (pas de nécessité de parenthèses pour les appels de fonctions et de sous-programmes) permet de donner des ordres ayant une vague allure de langage naturel. Les éléments IBM et AP, fournis avec ce workspace, sont simplement des matrices contenant des coordonnées de points respectivement en 2D et en 3D, la première colonne spécifiant une indication de tracé (couleur et style), les autres les coordonnées en x, y et éventuellement z. Des fonctions permettent également les entrées graphiques avec la souris ou le trackpad.

Quelques opinions

• Edsger Dijkstra

« APL is a mistake, carried through to perfection. It is the language of the future for the programming techniques of the past: it creates a new generation of coding bums ».

« APL est une erreur, poussée jusqu'à la perfection. C’est le langage de l’avenir pour les techniques de programmation du passé : il crée une nouvelle génération de fainéants du codage».

• Roy Keir

« APL is a write-only language. I can write programs in APL, but I can’t read any of them ».

« APL est un langage en écriture seule. Je peux écrire des programmes en APL, mais je ne peux en lire aucun. »

• Joel Moses

« APL is like a diamond. It has a beautiful crystal structure; all of its parts are related in a uniform and elegant way. But if you try to extend this structure in any way - even by adding another diamond - you get an ugly kludge ».

« APL est comme un diamant. Il a une superbe structure cristalline ; toutes ses parties sont en correspondance d’une façon uniforme et élégante. Mais si vous essayez d’étendre cette structure de quelque façon que ce soit — même en y ajoutant un autre diamant — vous obtenez un bricolage hideux ». (Allusion au passage d’APL à APL2).

• Jacques Arsac

« Je ne recommanderais pas de mettre rapidement APL entre les mains des étudiants[68] ».

Le professeur Arsac insiste en 1978 sur le fait qu'il ne remet nullement en cause l'intérêt du langage lui-même)[69]

Lisibilité

Épargnant l’usage des indices et des boucles en multipliant les opérateurs, APL permet l'écriture rapide et concise d'expressions ou de programmes qui seraient bien plus longs avec un langage classique. Vu la compacité et la puissance du langage, quelques puristes ont considéré un temps que pour être « élégant », un programme APL ne devait pas dépasser une ligne de code. Ces programmes, nommés one-liners dans la revue de l'ACM APL Quote-Quad étaient les ancêtres des deulignes[70] de ce qui sera plus tard Hebdogiciel.

Quelques problème récréatifs étaient parfois posés. Par exemple « comment effectuer la somme des éléments d'un tableau A (en principe +/A) quand les touches + et / ne fonctionnent pas ? ». Une réponse possible était 1⊥A (évaluation de A comme un nombre exprimé en base 1 !). Un autre était : "trouver la façon la plus concise de calculer la moyenne d'un vecteur V (ordinairement noté (+/V)÷⍴V) avec pour réponse V⌹V=V.

Cependant, la multiplicité des glyphes, leur usage unaire ou binaire, les superpositions de caractères censées les exprimer à l'époque des terminaux électromécaniques[71] ont fait qualifier ce langage de cryptique. L'absence de mécanismes conditionnels amenait par ailleurs chacun à employer diverses astuces nuisant à la lisibilité et à la maintenance des applications, sauf à introduire des fonctions au nom aussi parlant que possible.

           ⎕cr 'if'
z←a if b
z←b/a   
      'bonjour' if 1<0
      'bonjour' if 1<3
bonjour

Questions de sémantique

Quelques cas très particuliers de sémantique partagèrent les différents éditeurs. Ainsi, si A, B et C sont trois vecteurs de trois éléments, doit-on comprendre l'expression A B C[2] comme un vecteur de vecteurs ayant pour éléments le vecteur A, le vecteur B et le scalaire C[2] ? Tel est le choix d'interprétation de NARS2000. C'est également celui de GNU APL, comme celui d'IBM pour son APL2.

Dyalog, premier à introduire les tableaux de tableaux dans un APL commercial, avait alors fait le choix inverse et considérait l'expression comme équivalente à B. Bien qu'il suffise d'utiliser des parenthèses pour éviter toute ambiguïté, cet éditeur qui ne souhaitait pas introduire de problèmes de portage introduisit une variable système nouvelle, ⎕ML (migration level). Si cette variable est à 0, l'interprétation Dyalog s'applique. Sinon, c'est l'interprétation générale. Par ailleurs, la valeur de cette variable système peut être différente dans des fonctions différentes qui lui donnent une valeur locale (dans un écosystème de fonctions, par exemple), ce qui permet une interopérabilité souple.

Adressage associatif

APL n’a jamais officiellement connu les tables associatives, indexant un tableau avec autre chose que des valeurs entières, incorporées dans d'autres langages interprétés (Perl, Javascript, PHP...). On ne peut donc pas écrire :

CAPITALE[⊂'FRANCE']←⊂'PARIS'

ou, pour rester dans le vectoriel,

CAPITALE['FRANCE' 'ESPAGNE' 'ITALIE']←'PARIS' 'MADRID' 'ROME'

ce qui est contraignant, car :

1. une telle extension ne demanderait que très peu de modification de syntaxe, et n'en demanderait aucune des programmes existants ;
2. les langages modernes permettent l'indexation par des chaînes de caractères (soit l'indexation des tableaux comme en PHP qui autorise à écrire $capitale['France']='Paris';, soit via des objets voisins comme les tableaux associatifs en Perl[72]) ;
3. rares sont les applications où il ne faille pas gérer des accès par symboles plutôt que par numéros. Si APL ne le permet pas de façon immédiate, l’utilisateur se tourne naturellement vers d’autres langages répondant mieux à ses besoins.

Il est peu ergonomique de contourner cette lacune au prix de variables supplémentaires, par exemple : FRANCE←32 (dès lors, CAPITALE[FRANCE]←⊂"PARIS". Si le pays provient d'une saisie, l'indice peut être retrouvé par "execute" : ⍎"FRANCE" qui rend 32, mais l'application perd en robustesse et on encombre inutilement la table des symboles (APL/X contourne la difficulté par des namespaces).

Une autre manière est de définir un vecteur des noms de pays : PAYS ←'BELGIQUE' 'FRANCE' , l'instruction devenant alors : CAPITALE[PAYS⍳⊂'FRANCE']←⊂'PARIS'

Mais en ce cas, indépendamment de la lisibilité plus faible, le temps d'accès n'a plus le moindre rapport avec un accès direct de type « hash » en Perl ou PHP, surtout si s'il y a des centaines de noms. Non seulement la lisibilité des programmes n'y gagne rien, mais leur facilité de maintenance s'effondre compte tenu des variables surajoutées au programme.

Ce besoin est pris en compte dans les objectifs du projet NARS[73]. Dyalog APL permet de le contourner par son mécanisme non-standard des espaces de noms (namespaces)[74].

Approche objet et programmation fonctionnelle

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue ! Comment faire ?

Dyalog propose quelques espaces de travail et documentations PDF sur l'approche objet en APL, ainsi que sur la programmation fonctionnelle. Un exposé particulièrement clair sur APL en tant que notation algébrique rendue plus cohérente qu'en algèbre classique, et incluant des éléments de programmation fonctionnelle et effectué chez Google par Morten Kromberg est visible ici.

Essayer APL

Sans avoir besoin d'installer APL, on peut l'essayer sur cette page : http://tryapl.org/ pour frapper quelques expressions, les exécuter et en examiner le résultat (illustration de gauche).

Pour inclure dans la ligne de test les caractères APL de son choix, on les clique dans la partie de gauche de l'écran (onglet "Primer"). La variable système ⎕PP (printing precision) spécifie le nombre de décimales à afficher. D'autres variables sont ⎕IO (index origin, 0 ou 1), ⎕TS (time stamp, horodatage), etc. Des suggestions d'expression à exécuter sont proposées lorsque le pointeur de la souris passe au-dessus de tel ou tel caractère, entre autres les opérateurs de tri croissant et décroissant, ⍋ (grade up et ⍒ (grade down). La ligne frappée est exécutée lorsqu'on presse la touche Envoi (retour ligne), à la suite de quoi le résultat de l'exécution s'affiche et une nouvelle expression peut être introduite.

Cette page TryAPL est proposée par une société, Dyalog, qui autorise à télécharger gratuitement une version complète de son interpréteur (version 32 bits ou 64 bits) pour des usages personnels et non commerciaux. Chaque version gratuite est "tatouée" par un numéro de série attribué à titre personnel au demandeur. Pour les usages autres que personnels existent aussi des licences d'entreprise.

Documentation

PDF, téléchargeable

Français

• (fr) [PDF] APL vu du ciel, Bernard Legrand, AFAPL, 2006.

Anglais

• (en) Version anglophone du texte de Bernard Legrand ci-dessus
• (en) [PDF] Jeu complet des brochures de l'APL2 d'IBM
• (en) [PDF] Notes sur NARS2000
• (en) [PDF] Documentation de Dyalog APL

Vidéos

• Trois petits cours vidéo d'APL en français
• Jeu de la vie de Conway utilisant la programmation matricielle d'APL. Très spectaculaire.
• Introduction à APL… en 1975 (terminaux à boule sur mainframe).
• Conférences du concours APL 2014 et autres années de 2008 à 2016.
• 50 ans d'APL (plutôt orienté Dyalog APL, hormis le début)

Livres

Usage du langage

• S. Pommier, Introduction à A.P.L., Dunod, 1978 (ISBN 2-04-010402-X)
  (Nom collectif d'une équipe de l'École nationale supérieure des mines de Saint-Étienne : Jean-Jacques Girardot, Serge Guibout-Ribaut, Bertrand Jullien, François Mireaux et Michel Nakache[75])
• Bernard Robinet, Le langage APL, Éditions TECHNIP, 1979
• Robert Caillibot, Marcel Dupras et Claire Girard, Programmation en langage APL, Les Presses de l'Université Laval, 1981
• (en) Sandra Pakin et James A. Brown, APL 2 at a Glance, Prentice-Hall, 1988 (ISBN 978-0-13-038670-0)

Fondements du langage

• (en) Federico Biancuzzi et Shane Warden, Masterminds of Programming, Conversations with the Creators of Major Programming Languages, O'Reilly, 2009. [chapitre Trois : entretien avec Adin Falkoff]
• (en) Kenneth Iverson, A Programming Language, John Wiley and Sons, (1962), lisible également en ligne.

Gestion des objets en interne

• [PDF] Thèse de Christian Bertin

Bibliographie

• Bibliographie SUDOC

Articles connexes

• GNU APL
• Langage J
• Scilab

Liens externes

• Comment écrire un interpréteur APL (thèse détaillant l'implémentation de l'interprète APL du T1600)
• Le langage APL sous Linux par Edmond Orignac, ENS Lyon
• (en) « Les origines d'APL »^{(Archive.org • Wikiwix • Archive.is • Google • Que faire ?)} (vidéo)
• (en) Archives de Vector, revue de la British APL Association. Articles généraux et échange de bonnes idées.
• (en) http://aplwiki.com/ : Wiki consacré au langage APL
• (en) APL en 50 fonctions
• Exploration d’un arbre en « depth-first ».
• Résolution d’un problème de sudoku.

Notes et références

• Portail de la programmation informatique

На других языках

[ru] APL (язык программирования)